2 Basics, Notation and Data Structures
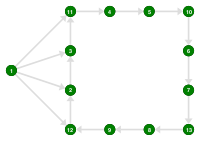
BFS-Components
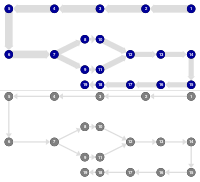
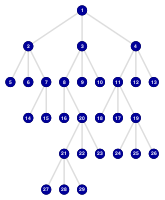
Finds connected components in a graph using iterated Breadth-First-Search (BFS).
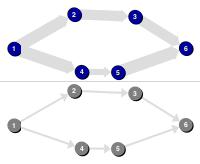
DFS Recursive
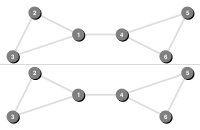
A recursive implementation of Depth-First-Search (DFS), which computes a DFS labeling.
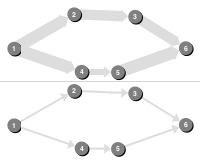
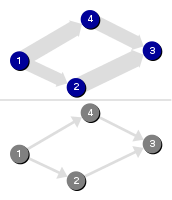
Iterative BFS
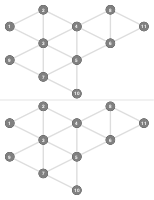
An iterative implementation of Breadth-First-Search (BFS), which computes a BFS labeling.
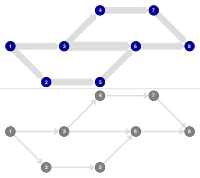
BFS to DFS
Converting the iterative BFS implementation to an iterative DFS implementation by exchanging the Queue for a Stack.
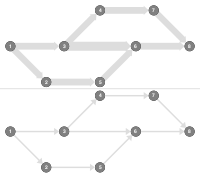
Iterative DFS
An iterative implementation of Depth-First-Search (DFS), which computes a DFS labeling.
3 Minimum Spanning Trees
4 Linear Programming Duality
Primal Dual of Kruskal's Algorithm
A primal dual version of Kruskal's Algorithm.
5 Shortest Paths
Dijkstra's Algorithm
Dijkstra's algorithm for finding a shortest path tree in a graph. This is an example of a label setting algorithm.
Dijkstra's Algorithm using a Priority Queue
Dijkstra's algorithm for finding a shortest path tree in a graph implemented using a Priority Queue.
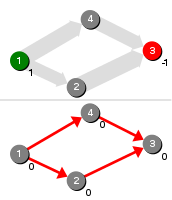
Find Path
A variant of Dijkstra's algorithm for finding a shortest s-t path in a graph. Terminates early, as soon as a shortest s-t path has been found.
Find Path in an Euclidean Graph
A variant of Dijkstra's algorithm for finding a shortest s-t path in an Euclidean graph (edge weights correspond to Euclidean distance between vertices). Terminates early, as soon as a shortest s-t path has been found and only visits a small part of the graph. Similar ideas are used in A*-type algorithms.
Bellman Ford
Bellman and Ford's algorithm for finding a shortest path tree in a graph with a label correcting approach.
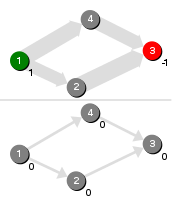
Finding Negative Circuits
Most shortest path algorithms require that graphs do not have negative circuits. This algorithms detects negative circuits in a graph.
Find Path from Two Sources
Finding a path can be accelerated by searching from start and destination simultaneously.
6 Maximal Flows
The Ford-Fulkerson Algorithm
The Ford-Fulkerson algorithm finds a maximal flow in a capacitated network by successive shortest path applications.
Preflow Push
The Preflow Push algorithm due to Goldberg and Tarjan computes a maximal flow by saturating a network and correcting possible excesses later.
7 Minimum-Cost Flows
8 Matching
9 Weighted Matching
Weighted Matching
This algorithm considers vertices as points in 2-dimensional space and implicitly assumes the existence of all edges in the complete graph. Furthermore, edge weights are Euclidean. It finds a matching of minimal weight. The matching is perfect if the number of vertices is even